Download Link
Wednesday, December 15, 2010
Standard Mathematical Tables and Formulae
Chapter 2: Algebra covers the different types of algebra studied: elementary algebra, vector algebra, linear algebra, and abstract algebra. Also included are details on polynomials and a separate section on number theory. This chapter includes many new tables.
Chapter 3: Discrete Mathematics covers traditional discrete topics such as combinatorics, graph theory, coding theory and information theory, operations re-search, and game theory. Also included in this chapter are logic, set theory, and chaos.
Chapter 4: Geometry covers all aspects of geometry: points, lines, planes, surfaces, polyhedra, coordinate systems, and differential geometry.
Chapter 5: Continuous Mathematics covers calculus material: differentiation, integration, differential and integral equations, and tensor analysis. A large table of integrals is included. This chapter also includes differential forms and orthogonal coordinate systems.
Chapter 6: Special Functions contains a sequence of functions starting with the trigonometric, exponential, and hyperbolic functions, and leading to many of the common functions encountered in applications: orthogonal polynomials, gamma and beta functions, hypergeometric functions, Bessel and elliptic functions, and several others. This chapter also contains sections on Fourier and Laplace transforms, and includes tables of these transforms.
Chapter 7: Probability and Statistics begins withbasic probabilityinformation(de n ingseveral common distributions) and leads to common statistical needs (point estimates, con d ence intervals, hypothesis testing, andANOVA). Tables of the normal distribution, and other distributions, are included. Also included in this chapter are queuing theory, Markov chains, and random number generation.
Chapter 8: Scientific Computing explores numerical solutions of linear and nonlinear algebraic systems, numerical algorithms for linear algebra, and how to numerically solve ordinary and partial differential equations.
Chapter 9: Financial Analysis contains the formulae needed to determine the return on an investment and how to determine an annuity (i.e., the cost of a mortgage). Numerical tables covering common values are included.
Chapter 10: Miscellaneous contains details on physical units (de nition s and conversions), formulae for date computations, lists of mathematical and electronic resources, and biographies of famous mathematicians.
Download Link
Fundamentals of Engineering
Units
Conversion Factors
Mathematics
Statics
Dynamics
Mechanics Of Materials
Fluid Mechanics
Thermodynamics
Heat Transfer
Transport Phenomena
Chemistry
Materials Science/Structure Of Matter
Electric Circuits
Computers, Measurement, And Controls
Engineering Economics
Ethics
Chemical Engineering
Civil Engineering
Environmental Engineering
Electrical And Computer Engineering
Industrial Engineering
Mechanical Engineering
Index
Tuesday, December 14, 2010
A Handbook of Statistical Analyses using SPSS
1 A Brief Introduction to SPSS
2 Data Description and Simple Inference for Continuous Data: The Lifespans of Rats and Ages at Marriage in the U.S.
3 Simple Inference for Categorical Data: From Belief in the Afterlife to the Death Penalty and Race
4 Multiple Linear Regression: Temperatures in America and Cleaning Cars
5 Analysis of Variance I: One-Way Designs; Fecundity of Fruit Flies, Finger Tapping, and Female Social Skills.
6 Analysis of Variance II: Factorial Designs; Does Marijuana Slow You Down? and Do Slimming Clinics Work?
7 Analysis of Repeated Measures I: Analysis of Variance Type Models; Field Dependence and a Reverse Stroop Task
8 Analysis of Repeated Measures II: Linear Mixed Effects Models; Computer Delivery of Cognitive Behavioral Therapy
9 Logistic Regression: Who Survived the Sinking of the Titanic?
10 Survival Analysis: Sexual Milestones in Women and Field Dependency of Children.
11 Principal Component Analysis and Factor Analysis: Crime in the U.S. and AIDS Patients’ Evaluations of Their Clinicians
12 Classification: Cluster Analysis and Discriminant Function Analysis; Tibetan Skulls
References
Download Link
Field Instrumentation Technical Handbook
Table of Contents
Conversions
Metric Values
Metric Prefixes
Temperature
Flow Rate
Miscellaneous
Equivalents
Liquid Measures and Weights
Kinematic Viscosity
Absolute Viscosity
Electrical Units
Degrees API and Degrees Baumé
Kinematic and Saybolt Viscosity
Pressure and Head
Properties
Density and Specific Gravity of Selected Liquids
Density and Specific Gravity of Selected Gases
Density and Specific Gravity of Saturated Water
Density of Superheated Steam and Compressed Water
Specific Gravity of Petroleum Products
Density of Air
Speed of Sound
Dielectric Constants of Liquids
Dielectric Constants of Solids
Viscosity of Gases and Vapors
Viscosity of Water and Steam
Viscosity of Various Liquids
Viscosity of Petroleum Products
Pipe Data
Dimensions of Blind Flanges
Flange Ratings by Class
Cast Iron Pipe
Steel Pipe
Even You Can Learn Statistics
Chapter 1 Fundamentals of Statistics
Chapter 2 Presenting Data in Charts and Tables
Chapter 3 Descriptive Statistics
Chapter 4 Probability
Chapter 5 Probability Distributions
Chapter 6 Sampling Distributions and Confidence Intervals
Chapter 7 Fundamentals of Hypothesis Testing
Chapter 8 Hypothesis Testing: Z and t Tests
Chapter 9 Hypothesis Testing: Chi-Square Tests and the One-Way Analysis of Variance (ANOVA)
Chapter 10 Simple Linear Regression
Chapter 11 Multiple Regression
Chapter 12 Quality and Six Sigma Applications of Statistics
Appendix A Calculator and Spreadsheet Operation and Configuration
Appendix B Review of Arithmetic and Algebra
Appendix C Statistical Tables
Appendix D Spreadsheet Tips
Appendix E Advanced Techniques
Appendix F Documentation for Downloadable Files
Glossary
Index
Download Link
Formulas and Conversions
Chapter 1 Definition and Abbreviations for Physical Quantities
Chapter 2 Unit of Physical Quantities
Chapter 3 System of Units
Chapter 4 General Mathematical Formulae
- Algebra
- Geometry
- Trigonometry
- Logarithm
- Exponents
- Complex Number
Chapter 5 Engineering Concept Formulae
Chapter 6 References
Download Link
Engineering Mathematics
Number and Algebra
Mensuration
Geometry and Trigonometry
Graph
Vectors
Complex Numbers
Matrices and Determinants
Boolean Algebra and Logic Circuits
Differential Calculus
Integral Calculus
Differential Equation
Statistic and Probability
Laplace Transform
Fourier Series
Index
Download Link
Dictionary of Mathematics Term
Preface vi List of Symbols
Mathematics Terms
Appendix
Algebra Summary
Geometry Summary
Trigonometry Summary
Brief Table of Integrals
download link
Basic Statistic Presentation
- Serves as a means to analyze data collected in the measurement phase.
- Allows us to numerically describe the data which characterizes our process’ KPIVs & KPOVs.
- Uses past process and performance data to make inferences about the future.
- Serves as a foundation for advanced statistical problem solving methodologies.
- Provides a language based on numerical facts and not intuition.
for complete presentation please download this link
Statistical Analysis using Excel
Chapter 1 Writing Formulae
Chapter 2 Copying and Cutting Formulae
Chapter 3 Paste Special
Chapter 4 Inserting Function
Chapter 5 Tracing Cell References and Debugging Formula Errors
Chapter 6 Function for Basic Statistic
Chapter 7 Probability Density Function and Confidence Interval
Chapter 8 Other Mathematical and Statistic Functions
Chapter 9 Add Ins Enhancing Excel
Chapter 10 Statistic Tools
Chapter 11 Hypothesis Testing
Chapter 12 Regression
Chapter 13 Other Tools for Statistics
Chapter 14 The Solver Tools for Constrained Linear Optimazion
Index
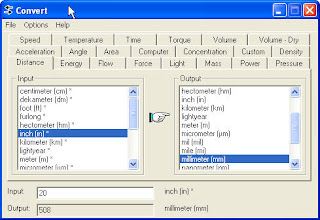
Convert version 4.8
- speed
- acceleration
- distance
- temperature
- angle
- energy
- time
- area
- flow
- torque
- computer
- force
- volume
- concentration
- light
- mass
- volume-dry
- density
- power
- pressure
Basic Concept of Mathematics
PrefaceAbout the Author
Chapter 1. Some Set Theoretical Notions
1. Introduction. Sets and their Elements
2. Operations on Sets, Problems in Set Theory
3. Logical Quantiers
4. Relations (Correspondences), Problems in the Theory of Relations
5. Mappings, Problems on Mappings
6. Composition of Relations and Mappings, Problems on the Composition of Relations
7. Equivalence Relations, Problems on Equivalence Relations
8. Sequences, Problems on Sequences
9. Some Theorems on Countable Sets, Problems on Countable and Uncountable Sets
Chapter 2. The Real Number System
1. Introduction
2. Axioms of an Ordered Field
3. Arithmetic Operations in a Field
4. Inequalities in an Ordered Field. Absolute Values, Problems on Arithmetic Operations and Inequalities in a Field
5. Natural Numbers. Induction
6. Induction (continued), Problems on Natural Numbers and Induction
7. Integers and Rationals, Problems on Integers and Rationals
8. Bounded Sets in an Ordered Field
9. The Completeness Axiom. Suprema and Infima, Problems on Bounded Sets, Infima, and Suprema
10. Some Applications of the Completeness Axiom, Problems on Complete and Archimedean Fields
11. Roots. Irrational Numbers, Problems on Roots and Irrationals
12. Powers with Arbitrary Real Exponents, Problems on Powers
13. Decimal and other Approximations, Problems on Decimal and q-ary Approximations
14. Isomorphism of Complete Ordered Fields, Problems on Isomorphisms
15. Dedekind Cuts. Construction of E1, Problems on Dedekind Cuts
16. The Infinities. The lim and lim of a Sequence, Problems on Upper and Lower Limits of Sequences in E
Chapter 3. The Geometry of n Dimensions.
1. Euclidean n-space, En Problems on Vectors in En
2. Inner Products. Absolute Values. Distances Problems on Vectors in En (continued)
3. Angles and Directions
4. Lines and Line Segments, Problems on Lines, Angles, and Directions in En
5. Hyperplanes in En, Linear Functionals on En, Problems on Hyperplanes in En
6. Review Problems on Planes and Lines in E3
7. Intervals in En, Additivity of their Volume, Problems on Intervals in En
8. Complex Numbers, Problems on Complex Numbers
9. Vector Spaces. The Space Cn, Euclidean Spaces, Problems on Linear Spaces
10. Normed Linear Spaces, Problems on Normed Linear Spaces
Notation
Index
download link
1001 Math Problems
Very useful math exercise book complete with the answer
Contents:
INTRODUCTION
SECTION 1 Miscellaneous Math
SECTION 2 Fractions
SECTION 3 Decimals
SECTION 4 Percentages
SECTION 5 Algebra
SECTION 6 Geometry
ANSWERS
download link
INTRODUCTION
SECTION 1 Miscellaneous Math
SECTION 2 Fractions
SECTION 3 Decimals
SECTION 4 Percentages
SECTION 5 Algebra
SECTION 6 Geometry
ANSWERS
download link
Subscribe to:
Posts (Atom)